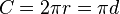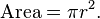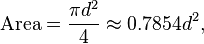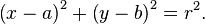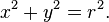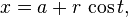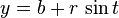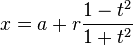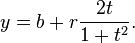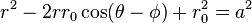صورة-1
الدائره (بالانكليزية: Circle) هى شكل بسيط فالهندسه الاقليدية. و تعرف بانها المحل الهندسى للنقاطالمتصله ببعضها البعض و الواقعه فالمستوي من علي بعد ثابت من نقطه ثابته ما ، و التي تسمي مركز الدائرة. المسافه الفاصله بين مركز الدائره و اي نقطه منها تسمي شعاعا او نص قطر.
الدوائر هى منحنيات بسيطه مغلقه تقسم المستوي الي جزئين : داخل الدائره و خارجها. فالاستخدام اليومي، ربما يستخدم مصطلح دائره للاشاره الي محيط الدائرة، و ربما يستخدم للاشاره الي ما يوجد بداخل الدائرة، و لكن بمعني ادق، فان الدائره هى المحيط فقط. اما ما يوجد فالداخل، فهو قرص.
الدائره هى حاله خاصه من الاهليلج حيث تنطبق بؤرتا الاهليلج مع مركز الدائرة. الدائره هى قطع مخروطى يحصل علية عندما يتقاطع مخروط قائم مع مستوي عمودى علي محور ذلك المخروط.
مصطلحات[عدل]
وتر و خط قاطع للقوس و مماس و قطر و شعاع.
قوس و قطاع و قطعة
نص قطر الدائره (قد يسمي شعاعها) هو الخط المستقيم الواصل بين المركز و اي نقطه من الدائرة. اما القطر فهو و تر الدائره المار من المركز و هو اطول اوتار الدائرة.
قطر الدائره هو قطعه مستقيمه تصل بين نقطتين من علي سطح الدائره و تمر بمركز الدائرة. و هو اكبر مسافه بين نقطتين اثنتين ما ، تقعان علي الدائرة. طول القطر هو ضعف طول الشعاع.
القوس هو جزء متصل من الدائرة.
القطاع هو المساحه المحبوسه بين شعاعين و القوس الذي يصل هذين الشعاعين.
الزاويه المركزيه للدائره هى الزاويه الذي يقع راسها فمركز الدائرة.
الزاويه المحيطيه هى الزاويه التي يقع راسها علي الدائره و يصبح ضلعاها و ترين فالدائرة.
الزاويه المركزيه تساوى ضعف الزاويه المحيطيه المرسومه معها علي القوس نفسه.
الزاويتان المحيطيتان المرسومتان علي قوس و احد فالدائره متساويتان.
الزاويه المحيطيه المرسومه علي قطر الدائره تساوى تسعين درجة.
و تر دائره هو اي قطعه مستقيمه تصل بين نقطتين ما تنتميان الي الدائرة. القطر هو اكبر و تر فالدائرة. مماس الدائره هو مستقيم يمس (او يتقاطع مع) الدائره فنقطه و حيدة، بينما المستقيم القاطع للدائره هو امتداد للوتر حيت يتقاطع معها فنقطتين اثنتين.
مركز الدائره هو النقطه الثابته المذكوره فالتعريف اعلاة و هى تقع فمنتصف الدائره بالضبط و عاده ما يرمز الية بالرمز (م) نسبه الي كلمه مركز.
مماس الدائره هو مستقيم يقطع الدائره فنقطه و احده فقط.
التاريخ[عدل] بعض من الاعوام المهمه فتاريخ الدائره :
فعام 1700 قبل الميلاد، اعطت و رقه قديمه تعود الي هذا الزمان كيفية تمكن من ايجاد مساحه الدائرة. تعطى هاتة الكيفية قيمه مقربه ل π و هى 256 / 81 (اى 3.16049…) .[1] فعام 300 قبل الميلاد، تحدث الجزء الثالث من كتاب اصول اقليدس عن خصائص الدوائر.
فالرساله السابعه لافلاطون، هنالك تعريف و شرح للدائرة.
فعام 1880، اثبت فيردينوند فون ليندمان ان π عدد متسام، ليحل و بشكل نهائى المعضله المطروحه منذ الاف السنين و المتمثله فتربيع الدائرة
نتائج تحليلية[عدل]
محيط الدائرة[عدل]
للمزيد من المعلومات، انظر الي بي.
عندما حاول العلماء القدامى، و علي راسهم غياث الدين الكاشي، اكتشاف قانون محيط الدائره احضروا دائره مصنوعه من الخيط بعدها فكوها و قاسوا الحبل فقالوا ان محيط الدائره هو طول قطعه الخيط المفكوكة. و عند اعاده نفس العمليه علي دوائر اخرى، لوحظ ان النسبه بين محيط الدائره (طول قطعه الخيط المفكوكة) علي القطر ثابتة. اي باختصار، قسمه المحيط علي قطر الدائره يساوى نفس الناتج رغم اختلاف الدوائر و محيطاتها و كانت النسبه تساوى تقريبا 3.141592654. وقد سميت تلك النسبه ط بالعربية[بحاجه لمصدر] و π (باي) باللاتينيه و ربما و ضحوا انه عندما يصبح قطر دائره مساويا ل1، يصبح محيطها مساويا ل π. محيط الدائره يساوى طول القطر x ط (π). هذة النسبه (ط) التي هى بين المحيط و طول القطر ثابته لاتتغير.
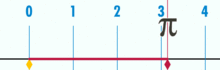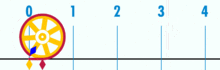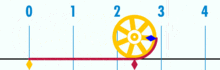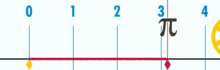
عندما يصبح قطر دائره مساويا ل1، يصبح محيطها مساويا ل π
- مثال علي محيط الدائرة
محيط دائره قطرها 7 سم = ط × طول القطر ≈ 7/22 × 7 ≈ 22 سم.
مساحه الدائرة[عدل]

مقاله مفصلة: مساحه القرص
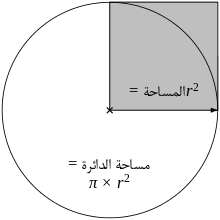
مساحه الدائره تساوي : 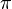
× مساحه المربع الملون
كيف عرفوا المساحه دون اضلاع.
احضروا دائره من قطع و رق مقوي و قسموها الي 8 اجزاء و قاموا لصق الاجزاء علي صوره مستطيل بحيث يصبح قطاع قوسة اعلي و احدث ملصوق بة قوسة لاسفل و عندما قاسوا مساحه المستطيل و جدوا ان الطول يساوى نص محيط الدائره و العرض يساوى نص القطر اي مساحه الدائره = مساحه المستطيل المصنوع منها.
ومنة نجد ان مساحه الدائره = نص المحيط × نص طول القطر (نق).
ولوضع ذلك قانون بدلاله نص القطر (نق)، نستطيع استعمال قانون (محيط الدائرة=ط × القطر).
وبالتعويض فقانون المساحه نجد:
مساحه الدائره = 1/2(ط × القطر) × نق
نقوم بضرب ال1/2 بما داخل القوسين، فنحصل على
مساحه الدائره = ط × 1/2القطر × نق
مساحه الدائره = ط × نق × نق = ط × نق تربيع.
اى ما يقارب 22/7 او 3.14 × القوه الثانيه لطول نص القطر (نصف القطر × نص القطر).
- مثال علي مساحه الدائرة
مساحه دائره طول نص قطرها 10 سم = ط × نق تربيع ≈ 3.14 × 10 × 10 ≈ 314 سم2.
الدائره هى المنحني المستوى الذي يضم المساحه القصوي (اكبر مساحة) عندما يصبح طول ذلك المنحني معروفا. ذلك يربط الدائره بمعضله فمجال حساب التغيراتوبالتحديد بمعضله متباينه المحيط الثابت.
معادلات[عدل]
الاحداثيات الديكارتية[عدل]
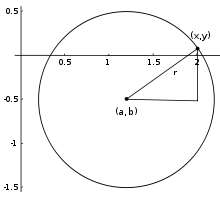
دائره شعاعها r = 1، و مركزها (a, b) المساوى ل 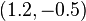
فى النظام الاحداثى الديكارتي، الدائره ذات المركز الذي احداثياتة هى (a، b) و شعاعها هو r، هى مجموعه النقط (x، y) حيث :
هذة المعادله تنبثق من مبرهنه فيثاغورس، عندما تطبق علي اي نقطه تنتمى الي الدائرة، كما يبين الشكل يساره. الشعاع هو و تر المثلث و المسافتان x – a و y – b هما طولا الضلعين الاخرين فالمثلث قائم الزاوية. اذا كان مركز الدائره هو مركز المعلم، فان هذة المعادله تصير اكثر بساطه كما يلي :
يمكن ان تكتب هذة المعادله علي شكل معادله و سيطيه (قد يطلق عليها اسم معادله بارامترية) باستخدام الدوال المثلثيه جيب و جيب تمام:
حيث t و سيط تتغير قيمتة بين العددين 0 و 2π. هندسيا، يمثل ذلك الوسيط الزاويه التي يكونها الشعاع المار من النقطتين (a,b) و (x,y) مع محور الافاصيل. المعادله الوسيطيه الاتيه تمثل كذلك دائرة:
الاحداثيات القطبية[عدل]
فى النظام الاحداثى القطبي، معادله دائره هى كما يلي:
حيث a هى شعاع الدائره و 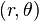
صورة-2
هى الاحداثيه القطبيه لنقطه ما من الدائره و
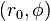
هى الاحداثيه القطبيه لمركز الدائرة.
المستوي العقدي[عدل]
فى المستوي العقدي، دائره مركزها هو c و نص قطرها هو r تمثل بالمعادله 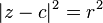
. و ربما تكتب هاتة المعادله بالشكل البارامترى الاتي : 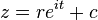
.